一致性哈希算法

在使用一致性哈希算法之前，首先我们要明确这个算法到底是用来做什么的，为什么要使用一致性哈希而不使用其他算法。

场景：

有4台服务器。每台服务器可以接受6个用户连接，现在有20个用户想要和服务器进行通信，我们该如何分配用户到不同的服务器上？

直接取模算法

第一步，我们为服务器标识唯一的ID，假设从0开始，则svrid为[0,3]

第二步，同理我们为每一个用户标识唯一ID，从0开始递增，则用户的id为[0,19]

第三步，我们使用最简单的取模算法，对id取模4(等于实际的服务器数量)后划分到不同的服务器上，可以得到以下的分配关系表

SvrId	UserID
0	0、4、8、12、16
1	1、5、9、13、17
2	2、6、10、14、18
3	3、7、11、15、19

这样解决了服务器能均匀的接受用户连接，只需要保证用户的userid是均匀分布的，

为什么userid需要均匀分布？

可以想象如果userid是不均匀的，比如userid=[0/4/8/12/16/20/24/28/32….]，取模后所有的user都会被分到svr0上，造成巨大的负载压力

如何扩容？

现在我们因为正常的服务器变动，需要将服务器的数量从4->5，仍然需要满足用户均匀的分配到各个服务器上，按照上节的取模方法重新建立的分配表如下

SvrId(服务器ID)	Pre(扩容前分配状态)	Aft(扩容后分配状态)
0	0、4、8、12、16	0、5、10、15
1	1、5、9、13、17	1、6、11、16
2	2、6、10、14、18	2、7、12、17
3	3、7、11、15、19	3、8、13、18
4		4、9、14、19

显然，为了满足分配的均匀性，我们需要变动的分配节点为16个，如果当前所有用户都已经和扩容前的服务器建立了连接，那么这一次扩容会导致80%(16/20)的用户出现断开连接并重新连接的情况，这个开销是我们没法容忍的

为什么一定要断开连接然后重新连接？

如果上述用户连接到服务器保持的是TCP的长连接，需要持续做DB写入等操作，就必须等待扩容前连接的服务器断开连接后，再重新建立连接到新的服务器，否则可能会出现两台服务器写入同一个DB数据，或者一个用户同时连接到两台服务器的情况(这显然违背了一致性原则)

代码实现

取模方法虽然扩容开销大，但是实现非常简单，也不需要存储任何数据，所有的用户在建立连接时可以通过接口直接知道应该连接哪个服务器

int GetSvrIDByUserID(int iUserID, int iSvrNum)
{
    if (iSvrNum == 0)
    {
        return 0;
    }
    return iUserID % iSvrNum;
}

一致性哈希算法

把数据用hash函数（如MD5，MurMurHash等算法），把userid映射到一个很大的空间里，找到离该数据落在的位置最近的下一个节点作为分配节点(简单起见就不画20个user节点了)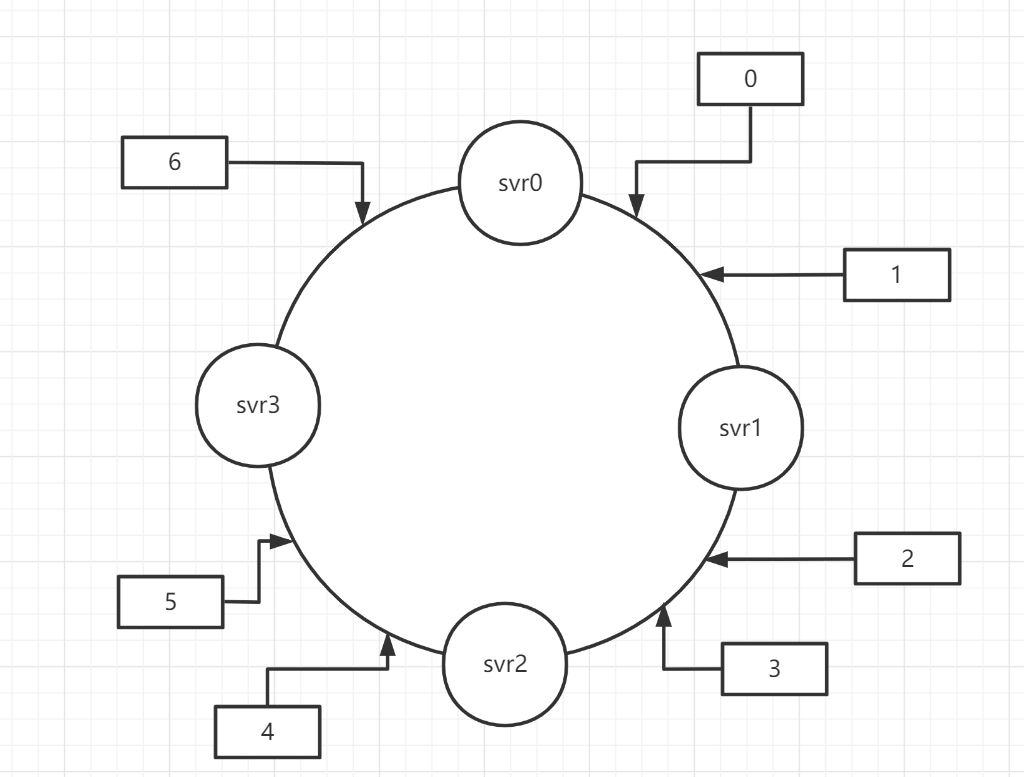

例如user0/1被分配到了svr1，user2/3分配到了svr2，有扩容需求时，我们同样将新加入的节点使用hash算法插入到环上，这样只影响svr插入位置之前的user节点的重分配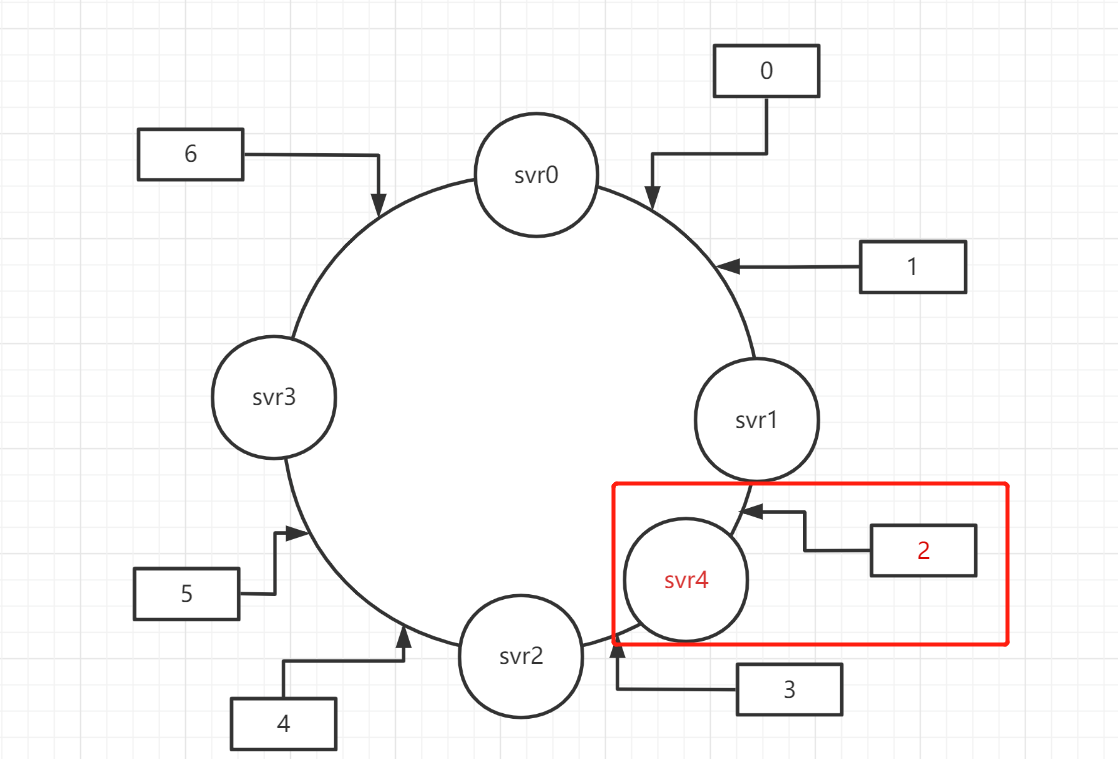

扩容前后的分配关系如下

SvrId(服务器ID)	Pre(扩容前分配状态)	Aft(扩容后分配状态)
0	6	6
1	0、1	0、1
2	2、3	3
3	4、5	4、5
4(新增)		2

分配不均

这种做法的明显弊端有两个：

1. 扩容时会存在某个svr部分持有节点转移到新svr,导致这两个svr的持有节点数量相较于其他svr明显不均匀
2. 缩容时某一个svr从环上撤下，则该svr原本持有的所有节点全部交给下一个svr，造成该svr负载两倍的压力

虚拟节点

既然把实际的svr节点放在环上不可取，我们可以建立虚拟节点解决扩容和缩容时出现的分配不均问题(假设现在我们为每个实际的服务器准备2个虚拟节点)

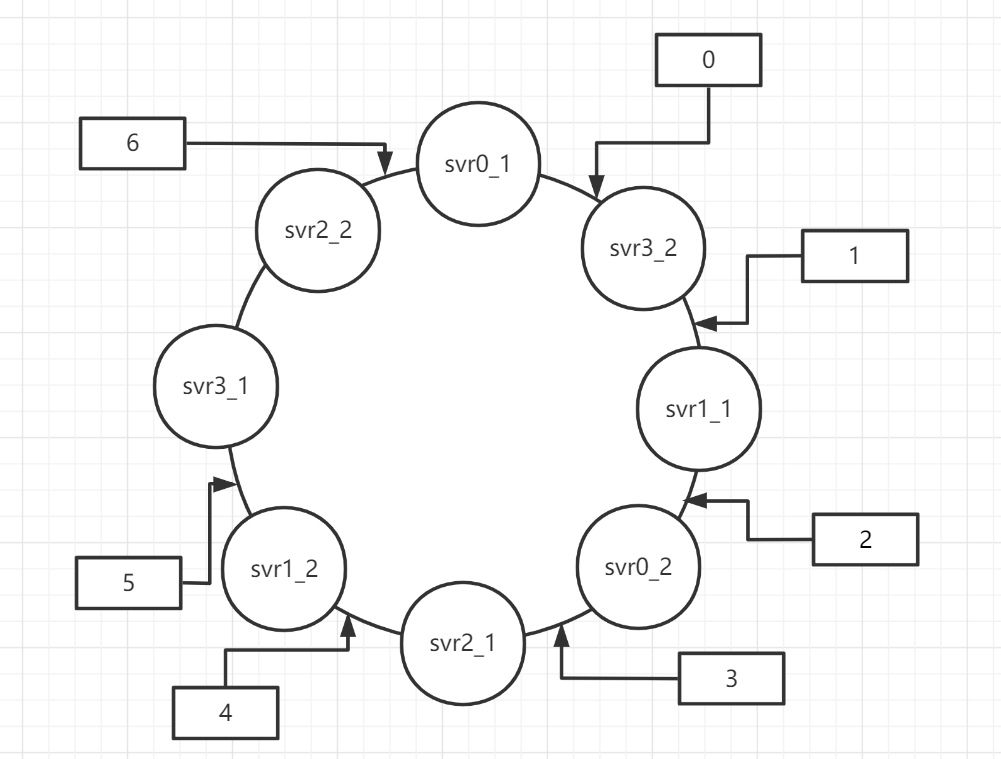
扩容的情况和不设置虚拟节点的方法类似，我们看缩容的情况，假设需要将svr0从环中取出，user节点在缩容前后的分配关系为

SvrId(服务器ID)	Pre(缩容前分配状态)	Aft(缩容后分配状态)
0(移除)	6、2
1	1、4	1、4
2	3	3、2
3	0、5	0、5、6

尽管可能还是存在分配不平衡，但是我们可以通过继续增加虚拟节点来缓解分布不均的问题

代码实现

因为有虚拟节点的概念，我们必须要维护一个虚拟节点-真实服务器的映射关系，并且在扩缩容的时候修改它

class ConsistentHash
{
public:
    ConsistentHash(int iRealNodeNum, int iVirtualNodeNum);


    int GetSvrIDByUserID(uint64_t userID);
    int HashKey(uint64_t);
    void DelNode(int iSvrID);
    void AddNode(int iSvrID);
    int GetNodeKey(int iRealID, int iVirtualID);

private:
    std::map<int, int> m_stServerNode; //虚拟节点和真实机器ID的对应关系
    int m_stVirtualNodeNum;//每一个真实机器拥有的虚拟节点数量
};
int ConsistentHash::GetNodeKey(int iRealID, int iVirtualID)
{
    return iRealID * 100000 + iVirtualID;
}
ConsistentHash::ConsistentHash(int iRealNodeNum, int iVirtualNodeNum)
{
    m_stServerNode.clear();
    m_stVirtualNodeNum = iVirtualNodeNum;
    //有iRealNodeNum真实服务器节点
    for (int i = 0; i < iRealNodeNum; ++i)
    {
        //每个真实节点都有iVirtualNodeNum个虚拟节点
        for (int j = 0; j < iVirtualNodeNum; ++j)
        {
            //这里将第i个真实机器的第j个虚拟节点转换成一个int类型的key,
            //怎么转换按实际需求来，简单起见这个函数就是做了下偏移
            int key = GetNodeKey(i, j);
            //虚拟节点对应到哪个真实服务器
            m_stServerNode[key] = i;
        }
    }
}
//扩容
void ConsistentHash::AddNode(int iSvrID)
{
    for (int j = 0; j < m_stVirtualNodeNum; ++j)
    {
        int key = GetNodeKey(iSvrID, j);
        m_stServerNode[key] = iSvrID;
    }
}
//缩容
void ConsistentHash::DelNode(int iSvrID)
{
    for (int j = 0; j < m_stVirtualNodeNum; ++j)
    {
        int key = GetNodeKey(iSvrID, j);
        m_stServerNode.erase(key);
    }
}
int ConsistentHash::HashKey(uint64_t uUserID)
{
    return (uUserID << 1) % 100000;
}
int ConsistentHash::GetSvrIDByUserID(uint64_t userID)
{
    //这里也是根据需要,自己做出userid到哈希环上位置的映射
    int key = HashKey(userID);
    map<int, int>::iterator it = m_stServerNode.lower_bound(key);//找到虚拟节点
    //未找到
    if (it == m_stServerNode.end())
    {
        return m_stServerNode.begin()->second;
    }
    //找到了
    return it->second;
}

jump consistent hash

一致性哈希算法的虚拟节点处理上有些复杂了，还是回到之前的问题，我们就想依靠真实的服务器节点，从4台扩容到5台，但是尽可能均匀的分配。

从结果分析，扩容前4台svr每台平均持有5个节点->扩容后5台svr每台平均持有4个节点，扩容过程中我们要做的是从原先已经分配的20个节点中选出4个转移到新增的第5台svr上

随机重分配

基于已经分配好的节点，我们对每个节点，让他有4/20的概率重新分配到新的svr上就好了(假设随机被选中的节点是7/10/13/16)

SvrId(服务器ID)	Pre(扩容前分配状态)	Aft(扩容后分配状态)
0	0、4、8、12、16	0、4、8、12
1	1、5、9、13、17	1、5、9、17
2	2、6、10、14、18	2、6、14、18
3	3、7、11、15、19	3、11、15、19
4(新增)		7、10、13、16

这样我们转移耗费的成本为20%(4/20)，对大多数用户都是没有影响

代码实现

现在我们考虑代码如何设计，保证不占用多余的内存，且扩容前后不改动代码

• 首先假设只有1台svr，此时所有节点都被放在svr0上
• svr增加到2台后，每一个userid都有1/2的概率被分到svr1上
• svr增加到3台后，每一个userid在之前的基础上有1/3的概率被分到svr2上
• …
• svr增加到n台后，每一个userid在之前的基础上有1/n的概率被分到svr(n-1)上

最后为了保证每次随机结果一样，我们需要使用userid作为随机种子

int GetSvrIDByUserID(int iUserID, int iSvrNum)
{
    if (iSvrNum == 0)
    {
        return 0;
    }
    srand(iUserID);//设置随机种子
    int iSvrID = 0;
    //模拟一个不断扩容的过程
    for (int i = 1; i < iSvrNum; ++i)
    {
        double rand_rate = 1.0 / (i + 1);
        double rand_result = ((double)rand()) / RAND_MAX;
        //每一轮有1 / (i + 1)的概率被分配到新的节点
        if (rand_result < rand_rate)
        {
            iSvrID = i;
        }
    }
    return iSvrID;
}

使用原则

我们需要去仿照虚拟节点的方式，建立起一种svrid到真实服务器的映射(例如IP)

扩容时，svrid必须从0开始，按顺序增大，不能像一致性哈希那样可以不按顺序新增

服务器真实IP	扩容前SvrID	扩容后SvrID
192.168.0.1	0(必须从0开始)	0
192.168.1.1	1	1
192.168.0.2	2	2
192.168.1.2	3	3
192.168.0.5(新增)		4（只能递增）

缩容时，被移除的服务器后面所有服务器的svrid都要 - 1

服务器真实IP	缩容前SvrID	缩容后SvrID
192.168.0.1	0(必须从0开始)	0
192.168.1.1	1	1
192.168.0.2(移除)	2
192.168.1.2	3	2
192.168.0.5	4	3

这种状态下，比如用户长连接中的信息就不能包含svrid，而只能包含ip(或者其他不会改变的可作为唯一索引的信息)，否则也会因为svrID的变化出现不一致问题

效率问题及优化办法

虽然上述算法已经可以满足要求，但是随着SvrNum的增大，计算SvrID的时间会越来越长，整个算法的复杂度为O(SvrNum)。
另有一点要注意，随着SvrNum越来越大，节点被重新分配的概率越来越小，无效的遍历也会越来越多

我们假设b表示跳变的svrid, 扩容到该svr时发生了跳变。j表示下一个跳变的svrid，从b开始持续扩容，直到j才发生新的跳变
则有i∈(b,j)，P(j >= i) = (b+1) / i
这个P是怎么来的？按照上一节代码中持续模拟扩容的过程我们可以知道，节点不重新分配到第i个svr的概率为
1 – (1 / (i + 1)) = i / i+1
那么从第b+1个svr到第i-1个svr连续不重分配的概率为
(b+1)/(b+2) * (b+2)/(b+3)… * (i-1)/(i) = (b+1)/i
此时我们取[0,1]上的一个均匀随机数r，且满足r<(b+1)/i
显然有i < (b+1)/r，可得i的上界限为(b+1)/r
又因为j>=i, 所以j的下界限为(b+1)/r
这样，我们就找到了从某一次重新分配svrid到下一次重分配svrid的转换公式为:
j = floor((b+1)/r)
使用这个公式可以确定每一次在哪一个svrid上重新分配了，就不用了遍历SvrNum次了。
我们假设user15这个节点在模拟扩容过程中从svr0->svr2，最终分配给了svr2

遍历轮次	0	1	2	3	4	5
老方案	0(初始分配状态)	1(不重新分配)	2(重新分配)	3(不重新分配)	4(不重新分配)	结束
新方案	0(初始分配状态)	下一跳是2(重新分配)	结束

int GetSvrIDByUserID(int iUserID, int iSvrNum)
{
    srand(iUserID);//设置随机种子
    int b = -1;
    int j = 0;
    while (j < iSvrNum)
    {
        b = j;
        double r = ((double)rand()) / RAND_MAX;
        //找到下一跳
        j = floor((b + 1) / r);
    }
    return b;
}

最终代码

实际论文中做了进一步优化，使用了线性同余发生器，代码最终如下

int32_t JumpConsistentHash(uint64_t key, int32_t num_buckets) {
    int64_t b = -1, j = 0;
    while (j < num_buckets) {
        b = j;
        key = key * 2862933555777941757ULL + 1;
        j = (b + 1) * (double(1LL << 31) / double((key >> 33) + 1));
    }
    return b;
}